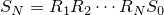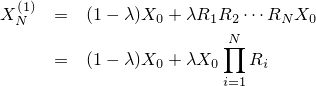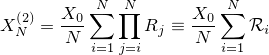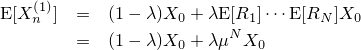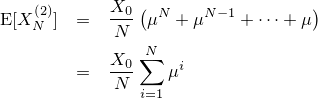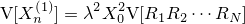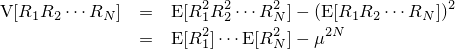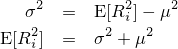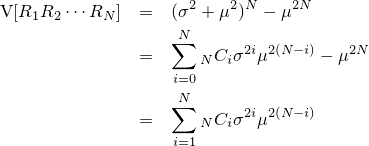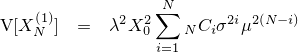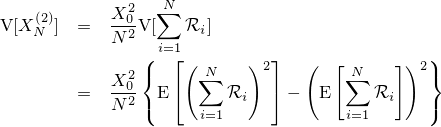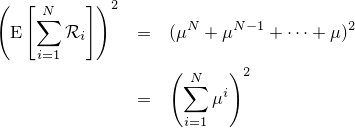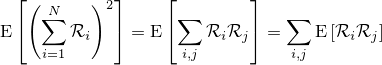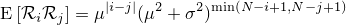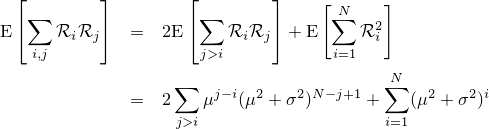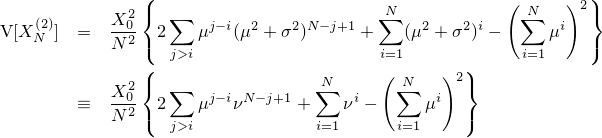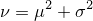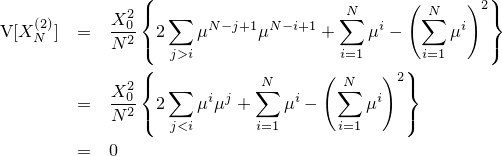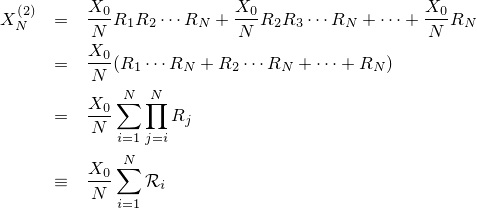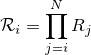ドルコスト平均法ははたして賢い投資方法と言えるのか？ part2

"Soviet poster of the transport sector during the Five Year Plan. 1930" by National Library of Scotland

3. 計算

前回の記事で株価が乗法モデル

に従った場合の一般投資戦略とドルコスト戦略の資産はそれぞれ

で与えられることが分かりました。

それではこれよりリスクの定量的評価を行います。私たちが知りたいのは、それぞれの資産のリスクとリターンの値です。この場合リターンは確率変数の期待値、リスクは確率変数の分散(より正確に言うと標準偏差)にそれぞれ対応していることが分かりますので、 X_N の期待値と分散をそれぞれ求めてやればよさそうです。

3.1 期待値の計算

まず簡単な期待値から調べていきましょう。 R_i と R_j は i≠j の場合独立であり、さらに R_i の期待値を μ 、分散を σ² と仮定しているため、 X_N⁽¹⁾ の期待値は

X_N⁽²⁾ の期待値は

となります。

3.2 分散の計算

次に一番知りたい分散についてですが、正直これは期待値に比べて少々面倒くさい。これは分散が期待値のような線形的な関係を持たない上に、ドルコスト平均法の R_i の項が折りたたまっているために生じているのですが、そんなことを憂いていても仕方がないのでさっさと計算していきます。

まず比較的簡単な X_N⁽¹⁾ の分散ですが、

ここで右式の V にのみ注目すると、分散の定義より

関係式

に注意すると、上式は

となりました。よって X_N⁽¹⁾ は

と表現できます。これは比較的何も悩まずに展開できました。

次にドルコスト戦略 X_N⁽²⁾ について同じように求めていきます。

2つの項が現れました。それぞれの項は結構面倒ですので、分けて考えることにします。まず第二項についてですが、

次に第一項について計算します。まず

ここで

についてそれぞれの R_k で乗算し、独立性から期待値を分割して求めるわけですが、きちんと注目してやると

• R_k となっている変数は全部で |i-j| 個
• R_k² となっている変数は全部で min(N-i+1, N-j+1) 個

となっているため、上式は

と展開できます。

ここで対称性について考えます。当たり前ですが i と j を反転させても上式の値は不変であるため、反転対称性から上式は以下のように展開できます。

以上から、 X_N⁽²⁾ の分散の値は

となります。ここで、数式を見やすくするために

と定義しておくことにし、便宜的にこの変数を『修正バリアンス』とでも名づけておきます。この命名が正しいのかどうか、そもそも名前がつけられているのかについてはよく分かりません。

この分散、和の項が3つ並んできたり少々面倒くさい形になっていますが、よくよく注目してみると σ に関して単調増加の形をしており、 σ=0 を代入すると結果に0が帰ってきたりとちゃんとしたリスク関数になっているのが確認できます。ただこの関数が一般投資戦略に比べてリスクを分散する形になっているかどうかはちょっと判別しにくいですね。

まぁそんなこんなで X_N⁽¹⁾ と X_N⁽²⁾ それぞれにおける期待値と分散を求めることができました。次回はこの関数を利用して定量的な調査を行っていきます。

Note. σに関して単調増加であることと0であることの説明

まず、式の形よりV_N⁽²⁾はσに関して単調増加関数であることは自明。
次にσ=0を代入すると修正バリアンスはμ²になるので、次数を調整した後で合計のラベリングを変更してやると、

となる。

ドルコスト平均法は賢い投資方法と言えるのか？ part1

"Soviet poster from the Five year plan showing economic investment. 1930" by National Library of Scotland

1. 概要

ドルコスト平均法という投資法があります。一応簡単に説明しておくと、ある区切られた期間ごとに同じ金額だけ対象の商品を購入しておくことで、安定した収益が得られるという戦略です。信託投資やFXをやっている方にとっては馴染み深い戦略かもしれませんし、ファイナンシャルプランナーからお勧めされた方も多いかもしれません。

一定期間同じ金額だけ同じ商品を買うだけというこの戦略、よく初心者にお勧めの投資法として雑誌などでは紹介されていますが、はたして本当にお勧めできる投資法なのでしょうか？またリスクを軽減できるとありますが、一体どれくらいのリスク軽減が望めるのでしょうか？それに対して、リターンはどれくらい減少するのでしょうか？以上を明らかにしていくのが今回の記事の目的です。

• 定量的に評価するために少々数式が登場してきますが、一応大学の経済学を専攻していたり、統計学について初歩的な知識(期待値や分散など)を持っている方ならばすいすいと読み進めることができるくらいのレベルを目指しています。
• 金融工学に関しての知識はまったく必要ありません。必要な箇所はすべて簡単に解説していきます。
• 今回の記事は式の導出までを行います。結果だけ知りたい方は読み飛ばしてもらっても構いません。

2. 2つの戦略

ここではドルコスト戦略についてより詳しく説明した後に、数式を用いて定式化していきたいと思います。今回は比較のため、ドルコスト戦略の他にもう一つ『一般投資』を取り上げていきます。

まず一般投資戦略とは特になんにも考慮することなく、自分の手持ち資産のうち一部分を対象の金融商品に投資して、その後は満期まで放置しておくという戦略です。

一方で、ドルコスト戦略はまず自分の手持ち資産のすべてをN分割し、一定期間毎に対象の金融商品を購入するという行為をN回行って、満期まで保持しておくという戦略です。

この2つの戦略を定式化する前に、まず以下の仮定を行っていきましょう。

1. 時間を離散化してN期間として考え、現在いる時点を0時点、満期をN時点とします。
2. 株価をS_nで表し、S_nは以下の『乗法モデル』に従うとします。
   
   
   
   
   ここで、R_iは確率変数とします。つまり、S_iも確率変数となります。ただし、S₀だけは現時点で株価が判明しているのでただの実数となります。
   R_i自体の確率分布は全く仮定していないことに注意してください。つまり、R_iは正規分布に従うとは限りません。
3. 計算を簡単にするため、異なる確率変数R_iとR_jは完全に独立であり、また期待値と分散は同一の値μとσ²を付与するものと仮定します。
   もちろん、これは理想化された仮定で、現実的ではありません。実際、R_iが過去の値に影響することは数々の測定から明らかになっています。が、そんなこといちいち考慮に入れるととっても大変ですし、そもそも今回の目的とは趣向が異なります。そこまで正確にやるんでしたら連続時間と仮定して確率微分方程式を解くべきですしね。こういうことするのは専門家だけで結構ですので今回はやりません。

以上の仮定を用いて、実際に2つの戦略を定式化します。まず一般投資戦略の場合、X_nをn時点での手持ち資産と定義すると、以下のように表せます。

ここで、λは手持ち資産のうち投資にかけるウェイトとして定義され、0<λ<1の間をとります。

次に、ドルコスト戦略の場合は、少々複雑ですが以下のように表せます。

ただし、後の計算を楽にするため、

とおきました。

ここで注目しておきたいのが、上式の形です。R_Nの項が最も多く出現し、満期から現時点まで下がっていくにつれて出現回数が減少していくのが分かるでしょう。このことから何が言えるのかというと、『ドルコスト平均戦略は満期近くの株価の変動に最も大きな影響を受ける』ということです。つまり、初期時点で株価が上昇しても、満期近くに株価が大きく下落した場合、ドルコスト戦略を用いると資産がマイナスになってしまうのです。

もちろん、λ=1(全力投資)の場合の投資戦略よりはリスクは分散されていることは式の違いにより明らかです。それは確かなので、ドルコスト戦略はリスクを軽減する戦略であることは間違いありません。ですが、これはλの値を調整することで同じ効果を与えそうです。

ここから分かる結論としては、『ドルコスト戦略は満期近くに株価が大きく上昇すると予想した場合に効力を発揮する戦略である』ということです。ですが通常の場合ですと、満期近くの株価の変動なんて正直予想できるはずがありません(明日の株価ですら予想は難しいというのに)。ドルコスト戦略が初心者にお勧めできるという論調は少々疑問であります。

そうなると結局のところ、フィナンシャルプランナーがドルコスト平均法を進める主な理由は『商品を定期購入してくれる客を作り出す』ためである気がしてなりません。だって長期投資という名目の元で、給料の一定金額を毎月自分たちに差し出してくれて、しかもその回数分だけ手数料をいただける。これほど美味しい客はありません…

…いやいや、そう考えるのはまだ早い。もしかしたらきちんとリスクを定量的に評価した上で勧めているのかもしれません。となると次に気になってくるのが『一体どれくらいリスクが減少するのか、その上でリターンはどれくらい減少するのか』という点です。「どうしてもドルコスト平均法じゃないといけないんですか？最初っから投資額を抑えることもできるんじゃないですか？」という声がどこからか聞こえてきそうです。

疲れたので今日はここまで。次回から実際のリスクとリターンの評価を行っていきます。

2006年に発表されたイグノーベル賞の文学賞が面白い

"860 Hispanic literature; 869 Portuguese" by Helder da Rocha

2006年に発表されたイグノーベル賞の文学賞が面白いです。どういう論文かっていうと『無駄に難しい単語を多用したとき、そいつは知的に見えるかどうか』っていう論文で、まずタイトルからして "Consequences of Erudite Vernacular Utilized Irrespective of Necessity: Problems with Using Long Words Needlessly." 。完全にふざけてます。Summaryも秀逸で、これ言いたいだけにこの論文書いただろって思うくらい。面白かったので思わずノリでSummary部分を翻訳してしまいました:

必要性と無関係に使用される博学な専門的用語が導く結末：不必要に長い単語を使うことにおける問題
DANIEL M. OPPENHEIMER

執筆者にとって最も奨励されている書き方は、過度に複雑な語彙の使用を避けることだ。しかしながら、大多数の学生は知的な印象を与えようとして、わざと複雑な語彙を使おうとする傾向にある。この論文ではその戦略が効果的であるかどうか、その程度について調査する。実験1-3では語彙の複雑性について扱い、語彙の複雑性と知的に見える効果の間柄には負の関係性があることを調べる。この関係性は元の小論文の質や、小論文の内容がどうであるかや、参加者が最初に期待していた度合いについては関わらない。複雑性の負の影響については、文章の読解速度(fluency)を処理することによって調べた。実験4では直接読解速度について扱い、読解が難しくなる文章はより著者が知的でないと判断されることが判明した。実験5では読解速度を遅くする要因について調査した。以上より、読解が難しくなる文章は明らかに正解であると即座に判断できなくなるため、人々は読解する手がかりの少なさから、文章をあまり信頼しなくなる。事実、文章の本質に関わらない語彙というのは過度に文章を修飾してしまい、結果としてかえって反対の方向へ影響してしまう。これらの影響や、実際の応用についても議論した。Copyright 2005 John Wiley & Sons, Ltd.

適当な翻訳で勘弁！この教授は学生の無駄に難しい言い回しを多用したレポートに飽き飽きして書いたんです。間違いない。

でも、実際こういうのってよくあるよなぁとか思います。『齟齬』『蓋然性』『慚愧』とか使われても、あんま頭良さそうに見えません。最近の例でいいますと対談の際に用いられた『写像』でしょうか。これも別にここで使わなくても、十分に説明できましたし…

やっぱりイグノーベル賞は全体的に面白いです。こういうセンス日本にはないよなぁ。羨ましい限り。

Geant4をCernのリポジトリ経由でインストールする

 "ALICE - A Large Ion Collider Experiment at Cern" by dominikf

Geant4のインストールはソースコードをダウンロードし、ビルドを行うという手法が旧来の日本のページではよく書かれていますが、Debian系列(Ubuntu)のディストリビューションを使っているのであれば、いちいちそんな手間のかかることをしなくてもリポジトリ経由でインストールすることができます。こんな大容量のライブラリですと、ライブラリの依存関係を解決するだけでも大分かかっちゃいますしね。

で、aptを利用してGeant4をインストールするためには、現時点では以下の手順を踏んで行うのが一番楽ちんです。

1. Cernのリポジトリを新規に追加します。
   
   deb http://lcg-heppkg.web.cern.ch/lcg-heppkg/debian stable hep
   deb-src http://lcg-heppkg.web.cern.ch/lcg-heppkg/debian stable hep
   
   の2つを、Synapticかコマンドライン経由で追加してあげればいいでしょう。
2. apt-get updateでデータベースを更新します。もちろんそのときこの2つのリポジトリが信用できるのかどうかわかりませんので、aptさんは
   
   W: GPG error: http://lcg-heppkg.web.cern.ch stable Release: 公開鍵を利用できないため、以下の署名は検証できませんでした: NO_PUBKEY F464E3D84061544D
   
   のようなエラーを吐きます。そこで、これらの警告がでないようにしてやります。
3. コマンドラインを立ち上げて、
   sudo apt-get install cern-archive-keyring
と入力。

警告: 以下のパッケージは認証されていません!
  cern-archive-keyring
検証なしにこれらのパッケージをインストールしますか [y/N]?

と当たり前ですが聞かれるので、yを入力します。信用されていないリポジトリから鍵をインストールして警告を出さないようにするってあたりが、俺を信頼しろ感が出ててとっても素敵。
4. apt-get update でエラーが出ないことを確認してから、sudo apt-get install geant4でGeant4をインストールして、終了です。

自分の環境(Ubuntu 10.04)ではこの手法で特に問題なくインストールできました。多分Debianでも普通にインストールできると思います。

さて、次に環境変数の設定を行っていきます。ホームディレクトリの".profile"ファイルの末尾に以下を記述します。


export G4WORKDIR=${HOME}/work/g4

これを行うことで、Geant4のワーキングディレクトリを${HOME}/work/g4に設定します。${HOME}以下は各自適当なやつに変えてみてください。

また、Geant4の動作に必要なシェルの変数を書き出すためには、対象のシェル内で

source /usr/share/geant4/env.sh

と入力。きちんとG4WORKDIRが設定されていることを確認してください。