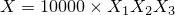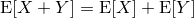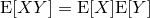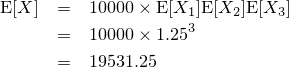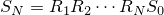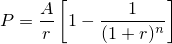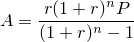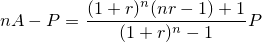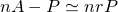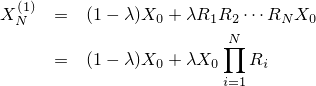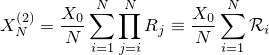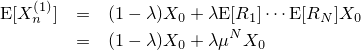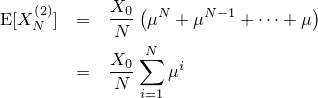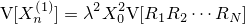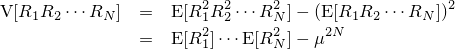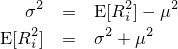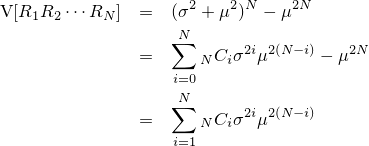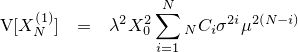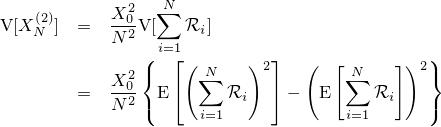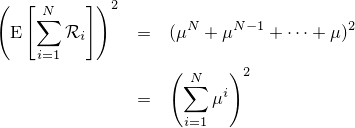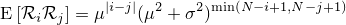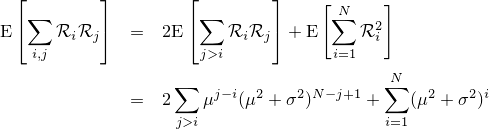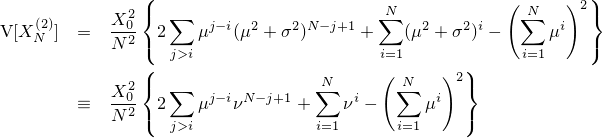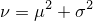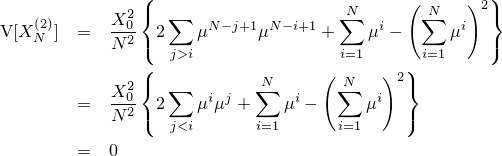『画像をぼかす』と一口に言っても、その方法にはいろんなものがあります。一番有名なのはPhotoshopの『ガウスぼかし』に見られるようなGaussian Blurですが、残念ながらこれはカメラに見られるようなリアルなぼかしと比べるとどうしても見劣りします。原因はいくつか考えられて、一つはGaussian Blurに使われているガウス関数の勾配が穏やかなため、現実のレンズのシチュエーションを考慮していないという点があります。
 |
| 左が元画像、中央がカーネルにガウス関数を用いた画像、右がフェルミ分布関数を用いた画像。 確かに中央よりは綺麗だけど、それでもまだリアルとは言えない |
画像をぼかすという行為は要は畳込み積分で、周囲のピクセル値を特定のウェイトで平均してやってることになります。で、普通にブラーしてしまうとピクセルの輝度に関わらず常に一定の割合で平均してしまいますので、なんか濁ったような画像が生成されてしまうと。
 |
| 通常のブラー。カーネルにはよりリアルに見せるため正六角形を用いている |
 |
| 結果の画像。比較的リアルにボカされていることが分かる |
 |
| 並べてみれば、違いがはっきり(クリックで拡大) |
 |
| 森林画像 |
 |
| 森林画像(通常のブラー) |
 |
| 森林画像(リアルブラー) |
 |
| 比較画像(クリックで拡大) |
#include <algorithm>
#include <cmath>
#include <string>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/core/operations.hpp>
struct exp_each_element
{
public:
exp_each_element(float factor): factor_(factor/256.0){};
cv::Vec3f operator()(cv::Vec3b &color) {
return cv::Vec3f(
std::exp(static_cast<float>(color[0])*factor_),
std::exp(static_cast<float>(color[1])*factor_),
std::exp(static_cast<float>(color[2])*factor_));
}
private:
const float factor_;
};
struct log_each_element
{
public:
log_each_element(float factor): factor_(factor/256.0){};
cv::Vec3b operator()(cv::Vec3f &color) {
return cv::Vec3b(
cv::saturate_cast<uchar>(std::log(color[0])/factor_),
cv::saturate_cast<uchar>(std::log(color[1])/factor_),
cv::saturate_cast<uchar>(std::log(color[2])/factor_));
}
private:
const float factor_;
};
cv::Mat make_fermi_kernel(float radius, float range) {
const int size = static_cast<int>(2.0*range + radius)*2 + 5;
const float mu = static_cast<float>(size/2);
const float range_inversed = 1.0 / range;
cv::Mat dst(size, size, CV_32F);
for(int i=0; i<size; ++i) {
for(int j=0; j<size; ++j) {
const float u = static_cast<float>(i - mu);
const float v = static_cast<float>(j - mu);
const float r = std::sqrt(u*u + v*v);
dst.at<float>(i, j) =
1.0/(std::exp(range_inversed*(r - radius)) + 1.0);
}
}
cv::normalize(dst, dst, 1.0, 0, CV_L1);
return dst;
}
cv::Mat make_regular_polygon_kernel(int number, float radius) {
const int size = static_cast<int>(2.0*radius) + 1;
const float center = static_cast<float>(size)/2.0;
std::vector<cv::Point> dst_vector;
for(int i=0; i<number; ++i) {
const float theta = 2.0*M_PI*i/number;
const cv::Point point = cv::Point(
center + radius*std::cos(theta),
center + radius*std::sin(theta));
dst_vector.push_back(point);
}
cv::Mat dst(size, size, CV_32F);
const cv::Scalar color(1.0, 1.0, 1.0, 1.0);
cv::fillConvexPoly(dst, &dst_vector[0], number, color);
cv::normalize(dst, dst, 1.0, 0, CV_L1);
return dst;
}
int main(int argc, char** argv) {
const std::string source = argc >= 2 ? argv[1] : "lena_std.tif";
const std::string destination = argc >= 3 ? argv[2] : "out.jpg";
const float factor = 6.0;
cv::Mat image = cv::imread(source);
CV_Assert(image.type() == CV_8UC3);
cv::Mat kernel = make_regular_polygon_kernel(6, 8.0);
cv::Mat exp_image(image.size(), CV_32FC3);
std::transform(image.begin<cv::Vec3b>(), image.end<cv::Vec3b>(),
exp_image.begin<cv::Vec3f>(), exp_each_element(factor));
cv::filter2D(exp_image, exp_image, -1, kernel);
std::transform(exp_image.begin<cv::Vec3f>(), exp_image.end<cv::Vec3f>(),
image.begin<cv::Vec3b>(), log_each_element(factor));
cv::imwrite(destination, image);
return 0;
}
余談
- 実質80行くらいで完成したので嬉しいです。可読性も多分結構読みやすい部類だと思う
- C++のコードが何やってるか分からない方は、まず関数オブジェクトとSTLについて調べてみましょう。あれはいいもんです
どんなデバイスであるか、たとえば、それが入力デバイスであるのか、出力でバイスであるのか、はたまた、計算処理デバイスであるのか次第で「輝度値の単位系」をどのように保持(処理)するべきかは違うことでしょう。
大切なことは、取り扱う「値」がどんな単位であるのかを見失わないことなのか、と思います。
hirax.net::「コンピュータ画像処理」と「輝度値の単位系」自分がこのような『任意の単調増加関数で良い』という具合で筆を進めたのには2つ理由があります。
まず1つ目が、『全てのデジタルカメラにおいて、ピクセルは輝度の対数の次元を取っているのだろうか?』という単純な疑問です。
きちんと物理的/工学的な意味合いを持つ画像処理にするためには、格納されているピクセルデータの次元がきちんと揃えられている必要があります。自分自身も普通に考えて輝度の対数が格納されているんだろうということで、任意ではなく指数関数に制限された関数系を使いましょうと運びたかったのですが、そうするための証拠が不足していた。
もしかしたら自分の予想もつかない方法で処理されている可能性があるわけで、そういった証拠が十分にないことから、単調増加関数と少し曖昧とした意味合いを含ませたのです。
もう一つの理由は『今回の画像処理は物理的に正確である必要がない』という理由です。これが大きかった。
そもそも今回の画像処理はどういう目的があるのでしょうか?ぼけて普通よりもリアルに見えて面白い、それで終わりです。物理的に計測をするわけではなく、ざっくり『それっぽく』見えればそれでいいという類のものです。そのような目的の下では、下手に物理的正確さを求めて処理時間を長くするよりは、計算速度の早いフェイクのほうがより適しています。
だから何も指数関数に制限する理由はあまりないわけで、より早くてよりそれっぽく見えれば、そちらのほうが優れていると、そう言えるわけです(ただ、今回の計算量からすると最も大きなオーダーとなっているのは畳み込み積分の箇所で、単調増加関数自体のコストはそれに比べれば微々たるものでしょう)。


%20%3D%20a(x,%20t)%7B%5Crm%20d%7Dt%20+%20b(x,%20t)%7B%5Crm%20d%7DW_t.png)
%20%26%3D%26%20a(x,%20t)%7B%5Crm%20d%7Dt%20+%20b(x,%20t)%7B%5Crm%20d%7DW_t%5C%5C%0Ay(t)%20%26%3D%26%20g(x,%20t).png)
%20%26%3D%26%20%5Cfrac%7B%5Cpartial%20g%7D%7B%5Cpartial%20t%7D%7B%5Crm%20d%7Dt%20+%20%5Cfrac%7B%5Cpartial%20g%7D%7B%5Cpartial%20x%7D%7B%5Crm%20d%7Dx%20+%20%5Cfrac%7B1%7D%7B2%7D%5Cfrac%7B%5Cpartial%5E2%20g%7D%7B%5Cpartial%20x%5E2%7D(%7B%5Crm%20d%7Dx)%5E2.png)
%5E2%20%26%3D%26%20%7B%5Crm%20d%7Dt%7B%5Crm%20d%7DW_t%20%3D%20%7B%5Crm%20d%7DW_t%20%7B%5Crm%20d%7Dt%20%3D%200%20%5C%5C%0A(%7B%5Crm%20d%7DW_t)%5E2%20%26%3D%26%20%7B%5Crm%20d%7Dt.png)
%20%3D%20%5Cmu%20x(t)%20%7B%5Crm%20d%7Dt%20+%20%5Csigma%20x(t)%20%7B%5Crm%20d%7DW_t.png)
%5E2%5C%5C%0A%20%26%3D%26%20%5Cfrac%7B1%7D%7Bx%7D(%5Cmu%20x%20%7B%5Crm%20d%7Dt%20+%20%5Csigma%20x%20%7B%5Crm%20d%7DW_t)%20-%20%5Cfrac%7B1%7D%7B2x%5E2%7D(%5Csigma%5E2%20x%5E2%20%7B%5Crm%20d%7Dt)%5C%5C%0A%20%26%3D%26%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)%7B%5Crm%20d%7Dt%20+%20%5Csigma%20%7B%5Crm%20d%7DW_t.png)
%20%26%3D%26%20y(0)%20+%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)t%20+%20%5Csigma%20W(t)%20%5C%5C%0Ax(t)%20%26%3D%26%20x(0)%5Cexp%5Cleft(%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)t%20+%20%5Csigma%20W(t)%20%5Cright).png)
%20%3D%20a(b-r(t))%7B%5Crm%20d%7Dt%20+%20%5Csigma%20%7B%5Crm%20d%7DW_t.png)
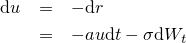
%5C%5C%0A%26%3D%26%20-%5Csigma%20e%5E%7Bat%7D%7B%5Crm%20d%7DW_t.png)
%20%26%3D%26%20v(0)%20-%20%5Csigma%20%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s%5C%5C%0A%26%3D%26%20b%20-%20r(0)%20-%20%5Csigma%20%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s%0A.png)
%20%3D%20r(0)e%5E%7B-at%7D%20+%20b(1-e%5E%7B-at%7D)%20+%20%5Csigma%20e%5E%7B-at%7D%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s.png)