はじめに
人工無能、一時期流行りましたねー。難そうなわりに以外と簡単で、しかも結果が面白いということでRubyやなんかで実装している記事をよく見かけました。そういった中でマルコフ連鎖が注目されていた時期が一時期ありましたが、正直あれはマルコフ連鎖を利用しているというよりは、別のアルゴリズムにマルコフ連鎖という名前をつけたというか、あんまり関連性がないなーという印象でした。
マルコフ連鎖の本質はそういうことではなく、状態の遷移確率を行列によって求めたり、定常分布を固有値問題で計算するところにある、と自分は考えています。マルコフ連鎖についてのより詳しい説明は他のブログにお任せするとして(自分がやるとすぐにボロが出てしまう)、今回はマルコフ連鎖を使って簡単な問題を解き、実際にマルコフ連鎖がどんな感じなのか確かめてみることにします。
もんだい
二つの箱A,Bが用意されている。2つの箱の内部は完全に遮蔽されており、外部からは確認することができない。また、Aの箱には赤玉がN個、Bの箱には白玉がN個入っている。
ここで、両方の箱に腕を突っ込み、それぞれの箱から玉を一個づつ取り出し、交換し、反対側の箱のなかに入れることにしよう。今回の場合、Aの箱には赤玉がN-1、白玉が1個入ることになる。もちろん、Bの箱には赤玉が1個、白玉がN-1個入っている。
この試行をひたすら続けて、そう、例えば無限回行ってみよう。この場合、Aの箱に入っている赤玉の数はどれくらいであろうか?個数に対応した確率分布を求めよ。
回答
1回、2回ならまだしも、無限回なんて計算できるかクソが!そんなふうに考えていた時期が俺にもありました。まず、Aの箱における赤玉の個数をmとおきます。すると、これは状態mの遷移問題と考えることができ、マルコフ連鎖が使えます。
また、1期間後にとりうることのできるmの遷移はm-1, m, m+1の3通りしか存在しません。以上を利用して、各mにおける状態の遷移確率を求めることができます。
まず、mがm+1に遷移する確率(m->m+1)を求めてみましょう。この場合、確率はAの箱の白玉が選ばれる確率とBの箱の赤玉が選ばれる確率の積に等しいので、
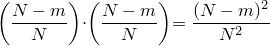
と表せます。
同様にして、m->m, m->m-1 についても表していきます。
- mがmに遷移する確率は(i)Aの箱の赤玉が選ばれる確率とBの箱の赤玉が選ばれる確率の積と(ii)Aの箱の白玉が選ばれる確率とBの箱の白玉が選ばれる確率の積 の和((i)+(ii))に等しい。
- mがm-1に遷移する確率は確率はAの箱の赤玉が選ばれる確率とBの箱の白玉が選ばれる確率に等しい。
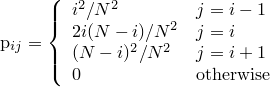
ここで、遷移行列はN×Nの次元を持っているものとします。
以上を利用して遷移行列を求め、pythonを用いて定常分布を算出しました。プログラムのソースコードを以下に示します。
#!/usr/bin/env python
#-*- coding:utf-8 -*-
"""
eig.py [N]
定常確率分布を記述したファイルを新しく書き込むプログラムです。
引数には箱に入っている玉の数を指定します。引数が指定されなかった場合には、N=10が用いられます。
"""
import sys
def main():
number = int(sys.argv[1]) if len(sys.argv) == 2 else 10
P = getStateMatrix(number)
result = getFiniteStateSpace(P)
fp = file("%i.dat" % number, "w")
fp.write("\n".join([str(abs(num)) for num in result]))
fp.close()
def getStateMatrix(n):
"""n個における遷移確率行列を返します"""
from scipy import matrix
P = [[getState(i, j, n) for j in xrange(n+1)] for i in xrange(n+1)]
return matrix(P)
def getState(i, j, N):
if j == i-1: return float(i*i)/(N*N)
elif j == i: return float(2*i*(N-i))/(N*N)
elif j == i+1: return float((N-i)**2)/(N*N)
else: return 0.0
def getFiniteStateSpace(mat):
"""
i->jに遷移する確率を行列(i,j)で表現した遷移確率行列から、定常分布を求めます。
この関数は行列を転置する必要がない点に注意してください。
mat : N×Nの遷移確率行列(numpyのmatrixでなければならない)
戻り値 : N次元の定常分布ベクトル
"""
from scipy import linalg
la, v = linalg.eig(mat.T)
result = zip(la, v.T)
# 定常分布を求めるため、固有値が1に近い順で固有ベクトルをソートする
result_sorted = sorted(result,
cmp=lambda x, y: cmp(abs(1.0-x), abs(1.0-y)),
key=lambda x: x[0])
eig_value = result_sorted[0][0]
# 固有値が1近傍でなかったら例外を送出
assert abs(eig_value - 1.0) < 1.0e-6, "the eigen value of FSS is apart from 1.0"
fss = result_sorted[0][1]
return fss/sum(fss) # 正規化
if __name__ == "__main__":
sys.exit(main())
実行は対象のソースコードを"eig.py"として保存してから、カレントディレクトリを適切なディレクトリに移動した後で、コマンドライン上から"python eig.py 10"のように指定してあげます。この場合、N=10(赤玉10個, 白玉10個)の際に遷移するであろう定常分布のデータが"10.dat"として書き出されます。
ここで、試しにN=6, 10, 50, 100における確率分布を載せておきます。
N = 6 のとき。離散的でよく分からないが、N=3付近の確率が一番高くなっている。
N = 10, 50 のとき。だんだん滑らかになっていく。
N = 100 のとき。N=50付近のピークが非常に鋭くなっている。
以上より、Nを増やせば増やすほど、N/2近傍により鋭いピークが表れるようになることが確認できます。
どーいうことが言いたいのか
結局のところ、お手玉の数を増やせば増やすほどmは中央付近で安定するわけです。「いや、最初に赤玉と白玉分けられているじゃん」それはそうなんですけど、今回の場合は無限回試行しているので、最初どのように分布してようが全く関係ないわけで。最初は偏っていた分布がごちゃごちゃやっている内に中央付近に移動し、そこから多少のゆらぎはあるかもしれないが、結果的に中央へと帰ってしまうような、そういうイメージです。















