"Aint they cute?" by Nicki Varkevisser
題名の通りで、以前から取り組んでおりました『OMakeマニュアル 日本語訳』の全ページを一つに纏めたPDFバージョンをリリースしました。
http://omake-japanese.sourceforge.jp/OMake.pdf
よりダウンロードできます。電子書籍でまとめてご覧になりたい方や、職場などの環境で使いたいけれどネットが使えないのでごりごり印刷したい…といった場合に便利です。
元々は渋川さんの『LaTeX経由でのPDF作成』という記事を拝見しまして、試験的にPDF版を作成してみたところ、思いのほか綺麗に製本されていることからきちんとリリースしてみようと思い立った次第です。殆ど素の状態から手を加えていないので暫定的ですが、後はきちんとスタイルを組んでいって、もうちょっと読みやすいレイアウトにしていけばいいかなって感じです。
思えば個人的な暇潰しから始まったこのプロジェクトも現在はPDFにして約200ページにもなり、きちんと一つの事柄に集中して取り組めたことは、学部時代のいい経験になったと考えています。まあ、これからも暇があればちょくちょくレイアウト、文章含めて修正していきますので、どうぞ今後ともよろしくお願いします。
2010/10/27
2010/10/04
確率微分方程式を解くー幾何ブラウン運動、バシチェックモデルの場合
"New York Fashion Week Fall 2007: Doo Ri" by Art Comments
確率微分方程式という分野がある。どういうものかっていうと、要は確率過程を微分方程式によって表そうという試みであり、微分方程式の中に微小の確率変数が含まれている。具体的にはこんな感じ。
%20%3D%20a(x,%20t)%7B%5Crm%20d%7Dt%20+%20b(x,%20t)%7B%5Crm%20d%7DW_t.png)
このdWはブラウン運動を表していて、時間がたつにつれてうねうねと確率的に動く。期待値と標準偏差はそれぞれ0と√tで、時間がたつにつれて動く場所もどんどん広がっていく。この運動はランダムウオークとか酔歩とも呼ばれていて、酔っ払ったおっさんがうねうねとあちこちに歩いているように見えることからこういう名前がついたそうな。上のような式で表すことができる確率過程を一般には『伊藤過程』と言って、他にもストラトノビッチ確率解析とかいうのもあるらしいけど、詳しくやっていないので分かりません。
これの何が便利かっていうと確率過程を通常の微分方程式のように扱えるところで、確率変数をまるで微分方程式を解くかのように求めることができる。とは言っても通常の微分方程式にはない規則がいくつかあって、初めはすごく奇妙に思えるかもしれない。
具体的には、以下のように確率変数x(t)とy(t)を定めた場合、
%20%26%3D%26%20a(x,%20t)%7B%5Crm%20d%7Dt%20+%20b(x,%20t)%7B%5Crm%20d%7DW_t%5C%5C%0Ay(t)%20%26%3D%26%20g(x,%20t).png)
このy(t)もまた伊藤過程に従い、確率微分方程式dyは以下のルールに従う。
%20%26%3D%26%20%5Cfrac%7B%5Cpartial%20g%7D%7B%5Cpartial%20t%7D%7B%5Crm%20d%7Dt%20+%20%5Cfrac%7B%5Cpartial%20g%7D%7B%5Cpartial%20x%7D%7B%5Crm%20d%7Dx%20+%20%5Cfrac%7B1%7D%7B2%7D%5Cfrac%7B%5Cpartial%5E2%20g%7D%7B%5Cpartial%20x%5E2%7D(%7B%5Crm%20d%7Dx)%5E2.png)
普通だったら消えるはずの2乗の項が残ってしまう。それじゃあ(dx)^2はどのようにして計算するのかというと、以下の公式に従う。
%5E2%20%26%3D%26%20%7B%5Crm%20d%7Dt%7B%5Crm%20d%7DW_t%20%3D%20%7B%5Crm%20d%7DW_t%20%7B%5Crm%20d%7Dt%20%3D%200%20%5C%5C%0A(%7B%5Crm%20d%7DW_t)%5E2%20%26%3D%26%20%7B%5Crm%20d%7Dt.png)
なんと、(dW)^2がdtに変化してしまう!これを『伊藤の公式』という。なんでそうなるのか?それを知りたい方は専門書を漁ればいくらでも載っているので、そこらへんを参照すればいいと思う。ここが通常の微分方程式と違うところで、逆を言えばそこさえ守ればきちんと積分によって求めることができる。専門書だとこの箇所がすごく分かり辛い表現で説明されているけど、詳細をはしょればこんな感じなはず。
それじゃあ、まず手始めに幾何ブラウン運動と呼ばれるモデル
%20%3D%20%5Cmu%20x(t)%20%7B%5Crm%20d%7Dt%20+%20%5Csigma%20x(t)%20%7B%5Crm%20d%7DW_t.png)
を求めてみる。これは株価の変動を表す最も簡単なモデルなんだけど、何故これが株価の変動を表しているのかっていうのは、とりあえず解いてみれば判明するはず。
さて、普通の考えだったら『変数分離法を用いてxを分離させて、そのまま積分すればよくね?』って発想になるんだけど、何度も言っているようにこれは確率微分方程式なので、まずは伊藤の補題を用いて変数変換を行い、xを分離させてみることにする。y = ln(x)とおくと、伊藤の補題より
%5E2%5C%5C%0A%20%26%3D%26%20%5Cfrac%7B1%7D%7Bx%7D(%5Cmu%20x%20%7B%5Crm%20d%7Dt%20+%20%5Csigma%20x%20%7B%5Crm%20d%7DW_t)%20-%20%5Cfrac%7B1%7D%7B2x%5E2%7D(%5Csigma%5E2%20x%5E2%20%7B%5Crm%20d%7Dt)%5C%5C%0A%20%26%3D%26%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)%7B%5Crm%20d%7Dt%20+%20%5Csigma%20%7B%5Crm%20d%7DW_t.png)
となる。(-1/2 σ^2)の項が出てくるところがミソで、普通に変数変換してしまうと出現しない。これで定数部分だけに分離できたので、そのまま愚直に積分を行うと、
%20%26%3D%26%20y(0)%20+%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)t%20+%20%5Csigma%20W(t)%20%5C%5C%0Ax(t)%20%26%3D%26%20x(0)%5Cexp%5Cleft(%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)t%20+%20%5Csigma%20W(t)%20%5Cright).png)
となる。これは対数正規分布の形となっているため、株価の変動を表す簡単なモデルとなっていることは容易に理解できると思う。
それでは、次にVasicekモデルと呼ばれるモデル
%20%3D%20a(b-r(t))%7B%5Crm%20d%7Dt%20+%20%5Csigma%20%7B%5Crm%20d%7DW_t.png)
について求めてみる。これは主に国債金利の利子率の時間的変動を表すモデルで、いったいこいつの何が重要なんじゃいっていうと、金融商品のリスクを推定する際に使われる。金融商品の価格は利子率によって変動するので、利子率の変動を推定することは金融商品のリスクを推定することに繋がる(*1)。つまり、今の自分のポートフォリオがどれくらいのリスクを持っているのか判断できる。そもそもこの記事を書くきっかけになったのはこいつが原因で、wikipediaさんにはただ『積分するとこれになりますよ』って書いてあるだけで、どうやって積分するのかについては書いていなかった。しょうがないので自分で手を動かして、ようやっと理解できたので公開してみようと。
さて、まずはu=b-rとおいて変数変換すると、
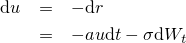
となる。ただ普通にChain Ruleやってるように見えるけど、たまたま結果が同じだっただけで、どんな変数変換でもきちんと伊藤の補題を使わなきゃいけない。そんで、物理やってる人はピンとくるかもしれないけど、これはランジュバン方程式の形となっているので、積分には同様の手法を利用できる。まぁ自分はピンとこなかったんですけど。それはさておき、v=e^(at)uとおいてさらに変数変換してやると、
%5C%5C%0A%26%3D%26%20-%5Csigma%20e%5E%7Bat%7D%7B%5Crm%20d%7DW_t.png)
となり、いい感じに余計な項が消えてブラウン運動だけになった。よってこれを積分してやると
%20%26%3D%26%20v(0)%20-%20%5Csigma%20%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s%5C%5C%0A%26%3D%26%20b%20-%20r(0)%20-%20%5Csigma%20%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s%0A.png)
あとはごちゃごちゃ整理してやると
%20%3D%20r(0)e%5E%7B-at%7D%20+%20b(1-e%5E%7B-at%7D)%20+%20%5Csigma%20e%5E%7B-at%7D%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s.png)
これでwikipediaさんにあるのとおんなじ形になった。めでたしめでたし。
なんかブログに書くと導出するのは楽ちんなように思えるけど、結構悩んだし大変だった。どんなもんでも答えを見るとすぐ分かるし思いつきそうなんだけど、実際になにもない地点から思いつくかどうかっていうのはまた別な話で、それを考えると新しい学問を生み出すっていうのは凄まじいほどの労力が必要だ。実際、未だにどういう発想で量子力学を思いついたのか本気で理解できない。あんなのヒントがいくらあっても無理だ。そういうことを考えた一日でありましたとさ。
*1: もちろんこの説明は適当でないが、詳しく説明してもあんまり意味がないのでこう書くことにする
追記(2010/10/04)
1/2の項が抜けていたので修正。
確率微分方程式という分野がある。どういうものかっていうと、要は確率過程を微分方程式によって表そうという試みであり、微分方程式の中に微小の確率変数が含まれている。具体的にはこんな感じ。
%20%3D%20a(x,%20t)%7B%5Crm%20d%7Dt%20+%20b(x,%20t)%7B%5Crm%20d%7DW_t.png)
このdWはブラウン運動を表していて、時間がたつにつれてうねうねと確率的に動く。期待値と標準偏差はそれぞれ0と√tで、時間がたつにつれて動く場所もどんどん広がっていく。この運動はランダムウオークとか酔歩とも呼ばれていて、酔っ払ったおっさんがうねうねとあちこちに歩いているように見えることからこういう名前がついたそうな。上のような式で表すことができる確率過程を一般には『伊藤過程』と言って、他にもストラトノビッチ確率解析とかいうのもあるらしいけど、詳しくやっていないので分かりません。
これの何が便利かっていうと確率過程を通常の微分方程式のように扱えるところで、確率変数をまるで微分方程式を解くかのように求めることができる。とは言っても通常の微分方程式にはない規則がいくつかあって、初めはすごく奇妙に思えるかもしれない。
具体的には、以下のように確率変数x(t)とy(t)を定めた場合、
%20%26%3D%26%20a(x,%20t)%7B%5Crm%20d%7Dt%20+%20b(x,%20t)%7B%5Crm%20d%7DW_t%5C%5C%0Ay(t)%20%26%3D%26%20g(x,%20t).png)
このy(t)もまた伊藤過程に従い、確率微分方程式dyは以下のルールに従う。
%20%26%3D%26%20%5Cfrac%7B%5Cpartial%20g%7D%7B%5Cpartial%20t%7D%7B%5Crm%20d%7Dt%20+%20%5Cfrac%7B%5Cpartial%20g%7D%7B%5Cpartial%20x%7D%7B%5Crm%20d%7Dx%20+%20%5Cfrac%7B1%7D%7B2%7D%5Cfrac%7B%5Cpartial%5E2%20g%7D%7B%5Cpartial%20x%5E2%7D(%7B%5Crm%20d%7Dx)%5E2.png)
普通だったら消えるはずの2乗の項が残ってしまう。それじゃあ(dx)^2はどのようにして計算するのかというと、以下の公式に従う。
%5E2%20%26%3D%26%20%7B%5Crm%20d%7Dt%7B%5Crm%20d%7DW_t%20%3D%20%7B%5Crm%20d%7DW_t%20%7B%5Crm%20d%7Dt%20%3D%200%20%5C%5C%0A(%7B%5Crm%20d%7DW_t)%5E2%20%26%3D%26%20%7B%5Crm%20d%7Dt.png)
なんと、(dW)^2がdtに変化してしまう!これを『伊藤の公式』という。なんでそうなるのか?それを知りたい方は専門書を漁ればいくらでも載っているので、そこらへんを参照すればいいと思う。ここが通常の微分方程式と違うところで、逆を言えばそこさえ守ればきちんと積分によって求めることができる。専門書だとこの箇所がすごく分かり辛い表現で説明されているけど、詳細をはしょればこんな感じなはず。
それじゃあ、まず手始めに幾何ブラウン運動と呼ばれるモデル
%20%3D%20%5Cmu%20x(t)%20%7B%5Crm%20d%7Dt%20+%20%5Csigma%20x(t)%20%7B%5Crm%20d%7DW_t.png)
を求めてみる。これは株価の変動を表す最も簡単なモデルなんだけど、何故これが株価の変動を表しているのかっていうのは、とりあえず解いてみれば判明するはず。
さて、普通の考えだったら『変数分離法を用いてxを分離させて、そのまま積分すればよくね?』って発想になるんだけど、何度も言っているようにこれは確率微分方程式なので、まずは伊藤の補題を用いて変数変換を行い、xを分離させてみることにする。y = ln(x)とおくと、伊藤の補題より
%5E2%5C%5C%0A%20%26%3D%26%20%5Cfrac%7B1%7D%7Bx%7D(%5Cmu%20x%20%7B%5Crm%20d%7Dt%20+%20%5Csigma%20x%20%7B%5Crm%20d%7DW_t)%20-%20%5Cfrac%7B1%7D%7B2x%5E2%7D(%5Csigma%5E2%20x%5E2%20%7B%5Crm%20d%7Dt)%5C%5C%0A%20%26%3D%26%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)%7B%5Crm%20d%7Dt%20+%20%5Csigma%20%7B%5Crm%20d%7DW_t.png)
となる。(-1/2 σ^2)の項が出てくるところがミソで、普通に変数変換してしまうと出現しない。これで定数部分だけに分離できたので、そのまま愚直に積分を行うと、
%20%26%3D%26%20y(0)%20+%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)t%20+%20%5Csigma%20W(t)%20%5C%5C%0Ax(t)%20%26%3D%26%20x(0)%5Cexp%5Cleft(%20(%5Cmu%20-%20%5Cfrac%7B1%7D%7B2%7D%5Csigma%5E2)t%20+%20%5Csigma%20W(t)%20%5Cright).png)
となる。これは対数正規分布の形となっているため、株価の変動を表す簡単なモデルとなっていることは容易に理解できると思う。
それでは、次にVasicekモデルと呼ばれるモデル
%20%3D%20a(b-r(t))%7B%5Crm%20d%7Dt%20+%20%5Csigma%20%7B%5Crm%20d%7DW_t.png)
について求めてみる。これは主に国債金利の利子率の時間的変動を表すモデルで、いったいこいつの何が重要なんじゃいっていうと、金融商品のリスクを推定する際に使われる。金融商品の価格は利子率によって変動するので、利子率の変動を推定することは金融商品のリスクを推定することに繋がる(*1)。つまり、今の自分のポートフォリオがどれくらいのリスクを持っているのか判断できる。そもそもこの記事を書くきっかけになったのはこいつが原因で、wikipediaさんにはただ『積分するとこれになりますよ』って書いてあるだけで、どうやって積分するのかについては書いていなかった。しょうがないので自分で手を動かして、ようやっと理解できたので公開してみようと。
さて、まずはu=b-rとおいて変数変換すると、
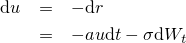
となる。ただ普通にChain Ruleやってるように見えるけど、たまたま結果が同じだっただけで、どんな変数変換でもきちんと伊藤の補題を使わなきゃいけない。そんで、物理やってる人はピンとくるかもしれないけど、これはランジュバン方程式の形となっているので、積分には同様の手法を利用できる。まぁ自分はピンとこなかったんですけど。それはさておき、v=e^(at)uとおいてさらに変数変換してやると、
%5C%5C%0A%26%3D%26%20-%5Csigma%20e%5E%7Bat%7D%7B%5Crm%20d%7DW_t.png)
となり、いい感じに余計な項が消えてブラウン運動だけになった。よってこれを積分してやると
%20%26%3D%26%20v(0)%20-%20%5Csigma%20%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s%5C%5C%0A%26%3D%26%20b%20-%20r(0)%20-%20%5Csigma%20%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s%0A.png)
あとはごちゃごちゃ整理してやると
%20%3D%20r(0)e%5E%7B-at%7D%20+%20b(1-e%5E%7B-at%7D)%20+%20%5Csigma%20e%5E%7B-at%7D%5Cint_%7B0%7D%5E%7Bt%7De%5E%7Bas%7D%7B%5Crm%20d%7DW_s.png)
これでwikipediaさんにあるのとおんなじ形になった。めでたしめでたし。
なんかブログに書くと導出するのは楽ちんなように思えるけど、結構悩んだし大変だった。どんなもんでも答えを見るとすぐ分かるし思いつきそうなんだけど、実際になにもない地点から思いつくかどうかっていうのはまた別な話で、それを考えると新しい学問を生み出すっていうのは凄まじいほどの労力が必要だ。実際、未だにどういう発想で量子力学を思いついたのか本気で理解できない。あんなのヒントがいくらあっても無理だ。そういうことを考えた一日でありましたとさ。
*1: もちろんこの説明は適当でないが、詳しく説明してもあんまり意味がないのでこう書くことにする
追記(2010/10/04)
1/2の項が抜けていたので修正。
Copyright 2009 映像奮闘記. Powered by
Blogger.
Blogger Templates created by Deluxe Templates
Designed by grrliz
Blogger Templates created by Deluxe Templates
Designed by grrliz


