保険商品の値段から入院する確率を算出してみた-02

前回の続きです。それでは計算によって求められた確率を載せたいと思います。

結果

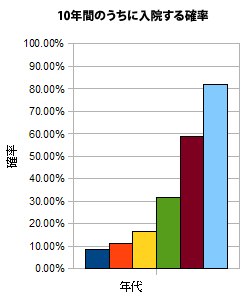
結果は以下のとおりです。保険料の金額は「価格.comの保険カテゴリ」で調べました。また、金融工学では通常ローンの利率を国債などの無リスク資産の年率で計算するので、今回はそれに合わせて日本の国債の年利1.37%を用いて計算しました（左上のボタンで全画面表示にできます）。

求められた確率をグラフで表すと以下のようになります。

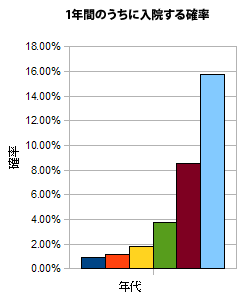
これではちょっと分かりにくいので、1年のうちに入院をする確率に補正してみましょう。10年間ずっと健康である確率をQとします。1年ずっと健康である確率Pがそれぞれ独立であり、すべて等しいと仮定すると、

P = Q^(1/10) (^はべき乗を表す)

となるので、これを用いて計算すると、

となりました。40代に入ってから、入院の確率が幾何級数的に増加していますね。

求めた確率は結局何を表しているのか？

前回の記事では2つの保険商品から1つの単純な賭けの問題に変形して確率を求めました。これは商品の値段ともらえる値段の期待値が等しくなる確率、言い換えると、「あなたも会社側も、お互い得も損もしない賭け事となる確率」です。この確率はお互いにとって中立であると言う意味で、金融工学では「リスク中立確率(Risk-neutral Probability)」といいます。

実際はそれだと会社側にとって利益がでないので、本当の確率は会社にとって有利な確率、つまりリスク中立確率よりも低い確率であると推測されます。

問題点

今回の計算では10年健康でいたら1回だけボーナスがもらえるという前提で計算をしたんですが、実際は保険料はそのままで、10年ごとに健康だったらボーナスをもらえるという商品なんです。そのため今回の計算だと、10年以降も健康でいる確率は考慮されていないわけです。これはわざわざ10年後に自分にとってさらに有利になる(保険料は同じなのに、歳を取るごとに入院する確率は増えるため)商品をわざわざ解約していることになるため、今回算出した確率は元からリスク中立でない、高めの確率を算出しているということになります。

で、その10年後の確率も考慮して解くってなるとちょい行列計算とか入って専門的になっちゃうんで、今回はやりません。ひまがあったらやってみます。

保険商品の値段から入院する確率を算出してみた-01

photo by wonderferret (creative commons license)

ちょっくら好奇心が沸いたので、金融工学を駆使して医療保険から入院をする確立を算出してみました。専門家にしか分からないような文章にしたらそもそもこれを書く意味がなくなってしまうので、あんま興味ない人や数学にあんま強くない人でもそれなりに楽しめるような内容を目指します。

それでは保険に関する簡単な説明をしたあと、確率のおーまかな算出方法を示して、それによる結果を提示していきます。結果は次回に載せるので、算出方法は興味ないけど結果はちょっと興味あるかもって人は今回は読まないほうがいいかも。

保険商品って？

保険にはダイヤモンドの輝きもなければ、
パソコンの便利さもありません。
けれど目に見えぬこの商品には、
人間の血が通ってます。

ていうCMが流れたことがありますが、結局のところ保険と言うのは金融商品の一種で、誤解を恐れずにいうならば、「自分が不幸になるほうにお金を賭けて、当たったらお金がもらえる商品」です。これによって不幸になったときの損失を減らし、万が一のときに備えることができるわけです。

このように金融商品を用いることで様々なリスクを回避したり低減しようとする手法を、一般に「リスクヘッジ(risk hedge)」といいます。金融工学はこのリスクヘッジ全般に対する理論体系が確立されているので、今回はこれを用いて入院する確率を算出してみます。

確率を算出するのに用いた商品

今回は確率の計算に「アリコのいっしょうおまかせ入院保険」のNAプランとNCプランを用いました。この保険は月払いで保険料を払い、もし

• 入院したら1日に1万円
• 手術になったらさらに10万円
• もし10年間入院しなかったらボーナスとしてNAプランなら10万円、NCプランなら20万円

がもらえる保険です。アリコ側は入院率をどれくらいで見積もっているんでしょうか？

新しく商品を作ってみる

その答えを出すためには、まずこの確率的に複雑な2つの商品をどうにかして単純な賭けの問題に変形する必要があります。そこでためしに次の例を考えてみます。

あなたはこの「自分が不幸になると得をする商品」を自由に売買できたとします。そこであなたはNAプランを1単位売って、NCプランを1単位買うことにしました。そうするとどういうことが起こるでしょうか？

• あなたはNCプランの保険料からNAプランの保険料を差し引いた分の金額を支払う必要があります。
• もしあなたが10年のうちに1回でも入院や手術になった場合、アリコ側からはNCプランの給付金がもらえますが、同時にあなたはNAプランの給付金を売った相手に支払う義務を負うことになります。つまりあなたの利益は±0ということになります。
• もしあなたが10年の間ずっと健康でいるならば、あなたは20万-10万=10万の利益を得ることになります。

これはつまり、2つの商品から「あなたが10年間健康でいれば10万の利益が得られる商品」を作ったことになります。この2つの商品の組み合わせで出来た商品を便宜上『健康プラン』と名づけることにします。

そしてこの健康プランは毎月同じ額の料金を支払う必要があります。これは毎月同額の料金を支払うという点で、車や住宅のローンと同じです。つまりこれは言い換えると「あなたはこの健康プランという商品を分割払いで買っている」ことになります。

いよいよ確率の算出

ここまでくればもうちょいです。あとはこの分割払いで買っている健康プランの値段はいったいどれくらいなのかを算出すればいいわけです。仮にこの健康プランの値段が8万円だったとします。健康だったときにもらえる金額は10万円ですので、この8万円を「10年間ずっと健康である確率の期待値」と見ると、その確率は

10年間ずっと健康である確率 = 8万円 ÷ 10万円 = 80%

となるため、逆に10年間のうち1回でも入院する確率は

100% - 80% = 20%

となるわけです。

長くなったので次回はその計算結果を載せたいと思います。ここまで読んでくれた人ありがとー！